通分の解説 2つの分数の分母を同じにすることを 通分 (つうぶん)と言います。 どうして分母を同じにする通分が必要になるかと言うと、分数同士の大小比較や計算(足し算や引き算)をするために通分がおこなわれます。 第 6 回のテーマは「 分数の概念と計算方法 」です。 割り算 , 割合 , 比の「 変形 」である「 分数 」についての話です。 今までの「 割り算 , 割合 , 比 」の知識 は、この「 分数 」を理解することで 全てが繋がり、完成します 。 分数は小数とも密接な関わりがあります。1分でわかる計算、割り算の仕方、問題の解き方 約分とは?1分でわかる意味、やり方、問題、約数、素因数分解との関係 まとめ 今回は、3つの分数の通分について説明しました。3つの分数の通分は「3つの分母が等しくなるような数を、各分数の分子と分母に掛け算」します。考え方は2
小学5年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生
分数の通分の仕方
分数の通分の仕方- 高校数学 通分の仕方 通分の仕方が分かりません。 2/3 4/5 とか y/x x/y とかなら通分できるのですが こんな文字がぐちゃぐちゃしたものを通分したことがないんで・・・しかも式が3つも・・・ 1時間かけたのですがどうやればいいのか本当に分かりません;; 誰か分かりやすく教えてください! お願いしますm(_ _)mまずは、逆わり算を使って24と36の最小公倍数を見つけましょう。 ちなみにそれぞれのパーツを見れば 何倍すれば最小公倍数になるのかも分かっちゃうから便利だよね。 それでは、それぞれの数に何を掛ければ最小公倍数になるのかも分かったところで通分して計算していきましょう。 完成! 通分を乗り切れば、計算自体は簡単だね (^^)! まとめ お疲れ様でした! 最小公倍数の求め方はこれでバッ
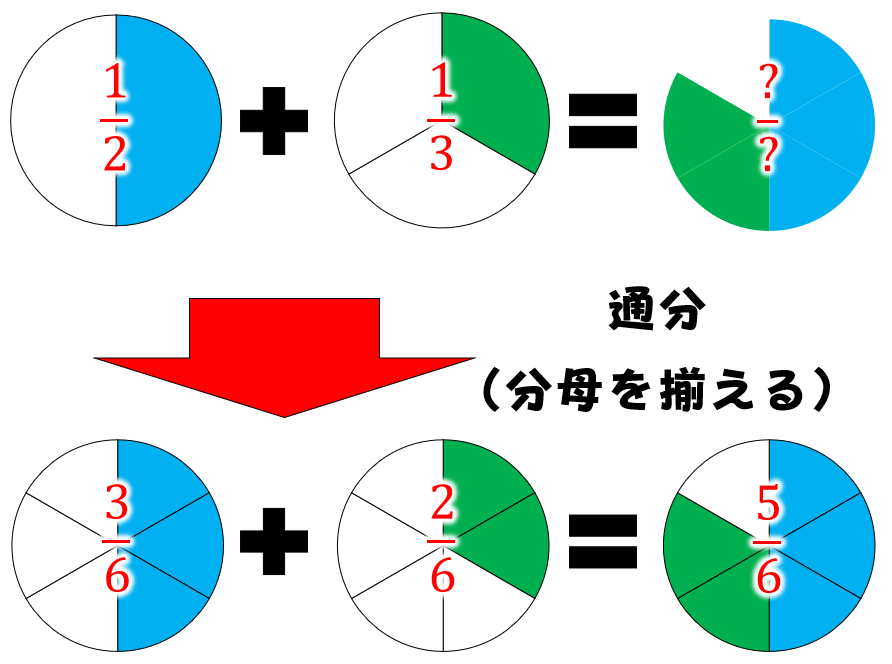



分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun
分母・分子の公約数を c c として、それぞれ a× c a × c 、 b× c b × c と表した時、分母・分子の差は (a− b)× c ( a − b ) × c で表せるため c c は約数となるのです。 具体的に 51 68 51 68 の例で見ると以下の通り。 68− 51=4 ×17 −3 ×17=(4−3) ×17=1× 17 68 − 51 = 4 × 17 − 3 × 17 = ( 4 − 3 ) × 17 = 1 × 17 51 85 51 85 の場合はこうなります。 分数の足し算 分数の足し算は ①:2つの分数の「分母」が同じになるようにそろえて(通分して)から ②:2つの分数の「分子」を足し算をして ③:最後に「約分」をする。 この 3つのステップをふむのがコツ です。 ここでは、「2/3 1/12」を計算してみましょう。分数分の分数のやり方 まとめ 分数の中に分数! こんな形が出てきたときには 上÷下 つまり、分子÷分母の計算を解いていけば 答えを出すことができます! 見た目は難しそうに見えますが 単純な割り算を計算するだけですからね
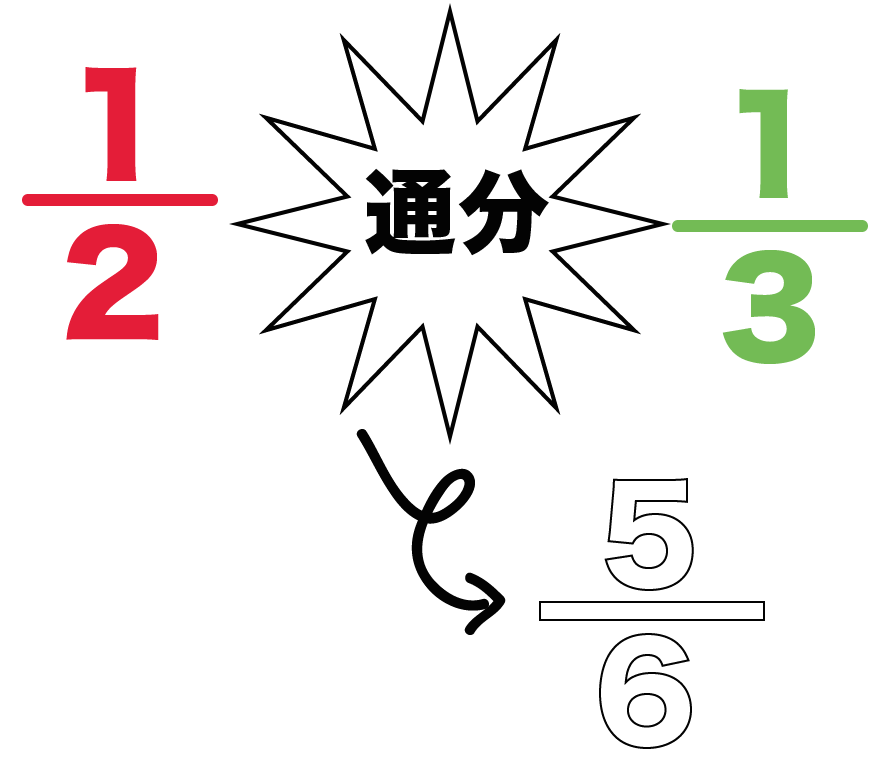
問題1 (2) 1 6 1 6 = ( 2) 1 6 1 6 = この問題も分母が同じなので、分子を足すだけで計算できます。 1 6 1 6 = 2 6 1 6 1 6 = 2 6 しかし、これだけでは終わりません。 2 6 2 6 は分母も分子も2で割れるため、 約分 する必要があります。 2 6 = 1 3 2 6 = 1 3 です。 よって、答えは 1 3 1 3 となります! 次が最後の問題です。分数の計算は大丈夫ですか? ここでちょっと補足です。 これから先は、分数の計算が頻繁に出てきます。 通分の仕方は大丈夫ですか? 小学生のときに習ったことですが、計算方法をマスター出来ずに中学生にあがってしまう人は少なくありません。 2と3の最小公倍数なので、6になります。 ②分母に何かをかけて、分母が最小公倍数になるようにします。 2分の1:2×3=6 3分の1:3×2=6 ③分母にかけた数と同じ数を分子にもかけます。 2分の1:1×3=3 3分の1:1×2=2 よって通分するとこうなります。 2分の1+3分の1=6分の3+6分の2 =6分の5 2人 がナイス! しています ナイス!
無学年で分数に関する演習をする計算プリントです。 進級テストつき!分数計算トレーニング (無学年) ・仮分数⇔帯分数 ・等しい分数 ・倍数/公倍数 ・約数/公約数 ・約分/通分 ・同分母たし算/引き算 ・分数のたし算/引き算 ・分数のかけ算 ・分数のわり算・10回のテスト形式で計算力を分数の足し算 通分(分母を同じにすること)します。分子同士を足し算します。約分します。 分数の引き算 通分(分母を同じにすること)します。分子同士を引き算します。約分します。 分数のかけ算 分子同士、分母同士をそれぞれ掛けます。計算途中で約分すると、最後に約分する手間を省けます。 分数の通分の計算の前に 私は、公文否定派で、百ます計算肯定派です。 とは言いましても、何から何まで公文がいけないというわけではなく、使い方の問題です。 ストップウォッチを使ってタイムアタックのように扱えう状況であれば、公文で良いです




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun




小学5年生の算数 分数の約分 通分 練習問題プリント ちびむすドリル 小学生
分数の通分"チョウ分数"|分子が1の場合 通分"チョウ分数"足し算(加法) チョウ分数の解き方の手順 ①分母と分母の間に、チョウのしっぽをかく。 ②ななめにちょうの羽根をかき、分子のほうに触角をかく。 分数の計算で、最も難しいのは通分です。 分母が違う分数どうしの計算ではよくミスしてしまうことも。 問題量も多いので、繰り返し練習して、マスターしてください。 今回はプロ塾講師が、アニメーション動画で、通分や約分の仕方を解説しています。分数÷分数 の計算 分数÷分数の計算のやり方を、例題を使って確認してみましょう。 1 2 ÷ 3 5 1 2 ÷ 3 5 を計算せよ。 分数の割り算は、割る数を逆数にして掛けることで計算できます。 この操作を、次の式の1行目から2行目で行っています。 1 2 ÷ 3 5 = 1 2 × 5 3 = 1× 5 2× 3 = 5 6 1 2 ÷ 3 5 = 1 2 × 5 3 = 1 × 5 2 × 3 = 5 6 このように計算することができます。




通分の新着記事 アメーバブログ アメブロ




3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく
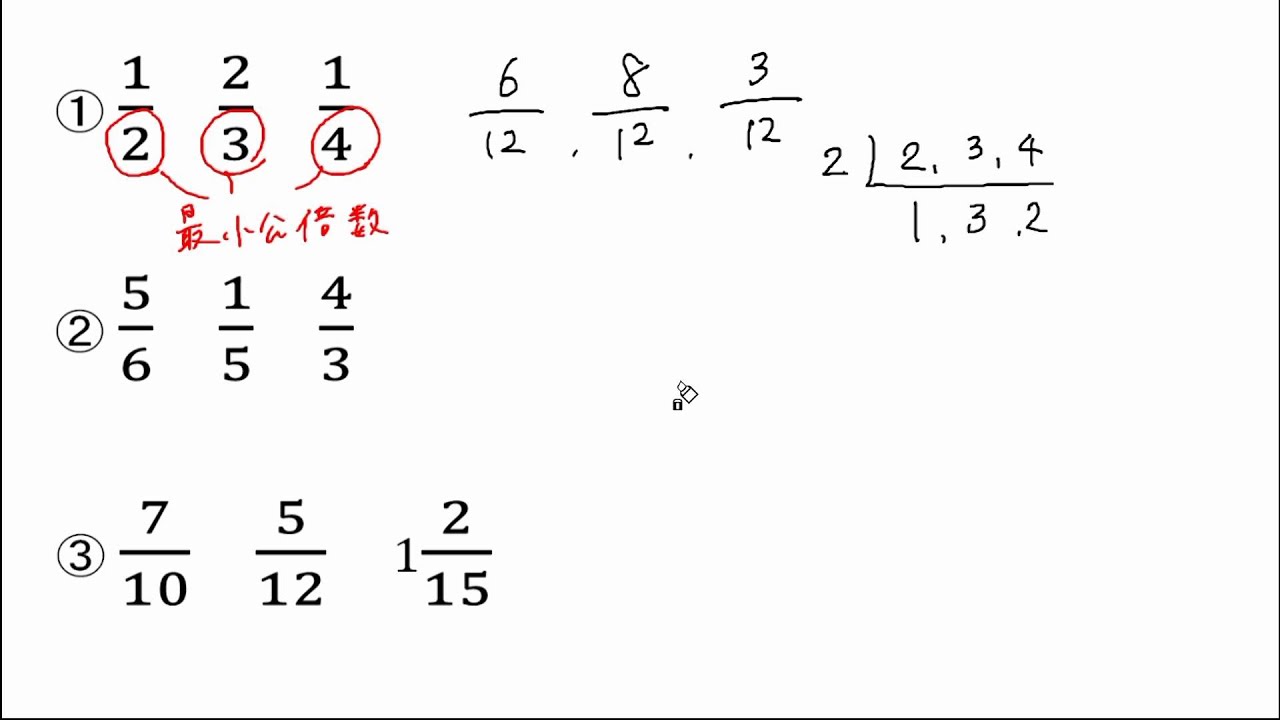
帯分数を仮分数に直す方法 まずは、1を分数で表すとどうなるのか考えてみましょう。 つまり、 分母の数と分子の数が同じならば「1」 になります。 では、他の整数はどうなるでしょうか。 つまり、 整数を分数に直すときは、「分子の数=分母の数×整数 」になります。 (例題1) に入る数字はいくつでしょう。 分子がいくつになるかを考えましょう。 整数を分数の中に分数が含まれる計算の解説 分数の中に分数が含まれるものの解法については主に2種類あります。 まず、ひとつめの割り算を使う解法です。 なんだよね。 だから、 です。 と分母分子を反対にした逆数をかければいいんだよね。 だから 次の分数を通分しましょう。 , , , , の分母の数は4,9,12。 4,9,12の最小公倍数は36なので、分母が36になるよう、それぞれの分子と分母に同じ数をかけます。 = = = = = = 答え , , スポンサードリンク




分数計算 手順が大事



5年算数 通分約分の仕方
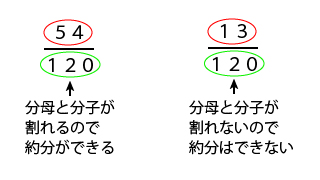
また、計算問題などの答えが、$\frac{\displaystyle 299}{\displaystyle 437}$のような、 分子も分母も3桁以上になるような分数 となった場合は、 約分が出来ると予測 されます。 ※ 全国の入試問題の統計をとったわけではないのですが 感覚論です。 通分のやり方はこちら⇒ 通分と約分やり方と問題 ②分子どうしを足す 分母をそろえたら、分子ど うしの 引き算をします。 ③約分する ②の引き算をしたあとに約分できる場合は、 約分 をして計算を終えます。 〈分母が同じ分数の引き算〉 分母がすでにそろっているので通分をする必要はありません。 分子ど うしの 引き算からはじめ、最後に約分ができる場合は約分をして計算を終分数の通分は、大きい方の分母の公倍数を最初にみつけ、それを分母とする分数になおすとかんたんです。 以上のことを確認したら、教科書の問題を解かせてみましょう。 このつづきはこちら ↑分数のたし算・ひき算 5年の目次に戻る トップへ戻る
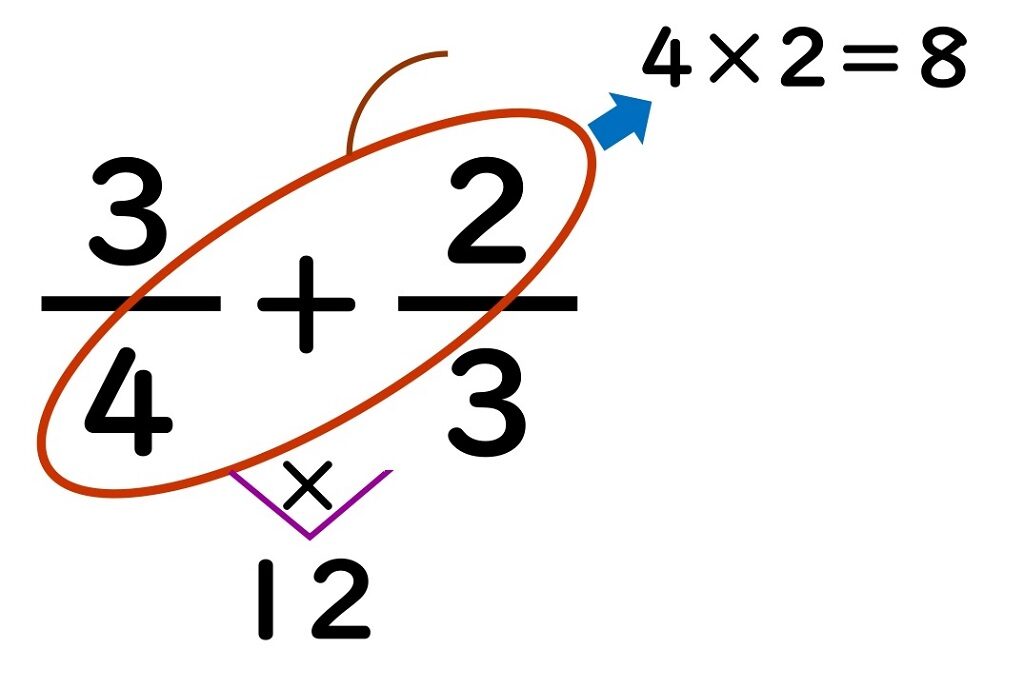



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説



小学5年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生
と計算していくのです。 簡単な通分の仕方 1番簡単な通分のやり方は、 相手の分母の数を自分の分母と分子に掛ける です。 具体的に解説していきます。 $$\displaystyle \frac{1}{3},\ \displaystyle \frac{1}{7}$$ この2つの分数を通分したいとします。 下の画像は 全て「1/2」と入力 した後に、「a2」は 分母を16に設定 、「a3」は 分母を100に設定 したものです。 自由に分数の書式を設定する方法(仮分数と帯分数) さらに自由に設定してみましょう。 仮分数→帯分数にするときは、 分子を分母で割った答えが帯分数の整数に。 あまりが、仮分数の分子です。 今度は、帯分数1 は、 が1つと ですから、 ×1 = 。 帯分数→仮分数にするときは、 整数の部分×分母分子が、仮分数の分子になります。 練習仮分数は帯分数に、帯分数は仮分数に直してみましょう。 (1) (2) (3) 1 (4) 1 (5) 2 答え (1) 7÷3=2あまり1→ =2 (2) 15÷4=3あま
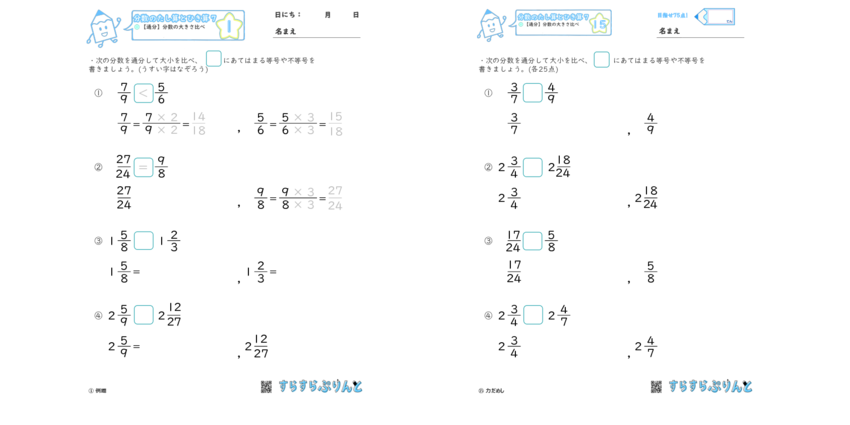



通分 分数の大きさ比べ 小学4年生算数 無料プリント教材




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ
2つ以上の分数式に対して,通分して加法・減法の計算ができる。 繁分数を簡単な分数式に表すことができる。 分数式の約分 分数(式)には,分母と分子に同じ数(式)を掛けたり,同じ数(式)で割ったりしても値が変わらないという性質 \\displaystyle \frac{A}{B} = \frac{A \times C}{B
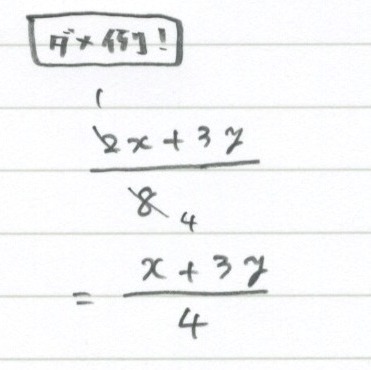



4 2 式の計算 約分の注意点 勉強できようサイト
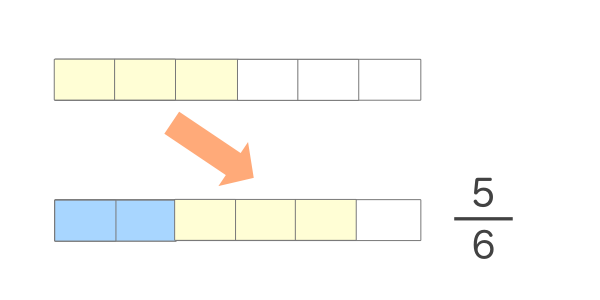



通分 計算が簡単にできる電卓サイト




文字が入った分数の足し算や引き算 分子にかっこをつけて通分する 中学や高校の数学の計算問題
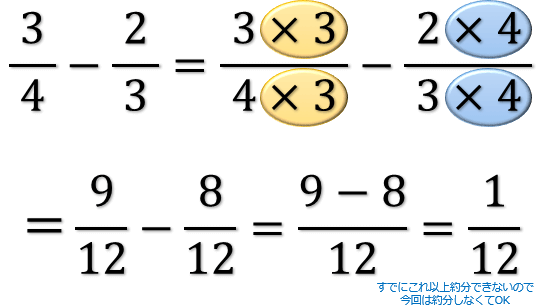



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ
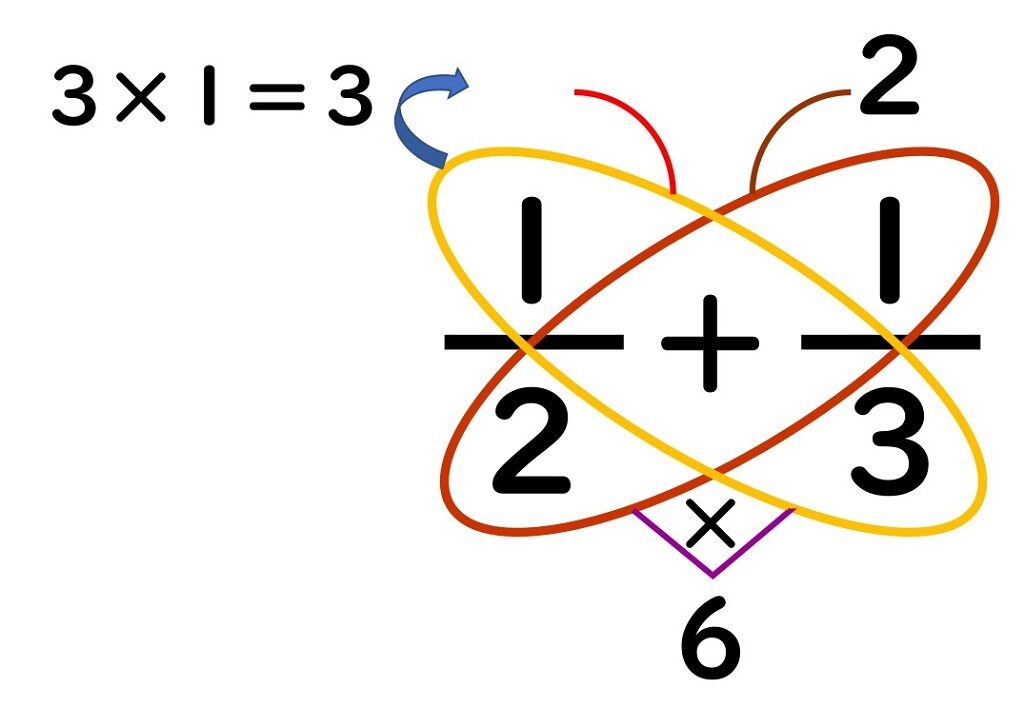



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説




分数を使いこなそう すだれ算って知ってる 後編 桜花 現役バイト塾講師 Note
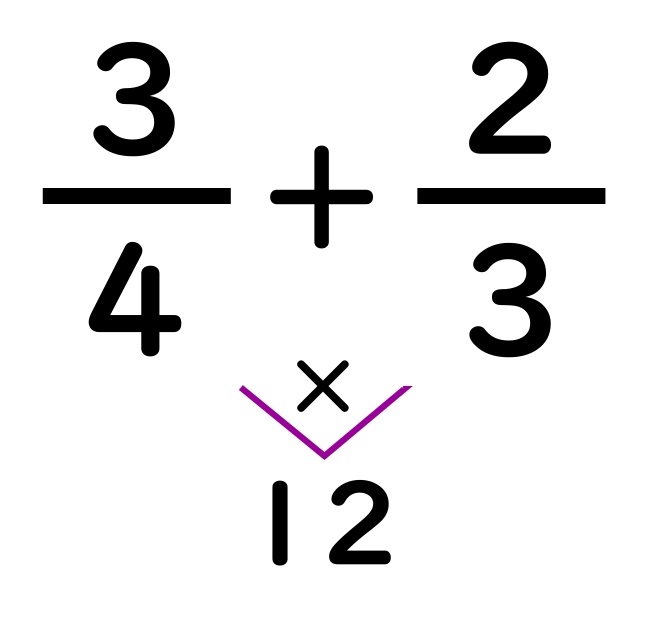



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
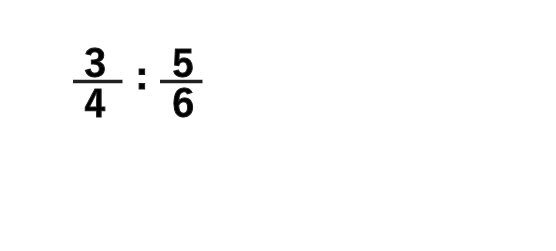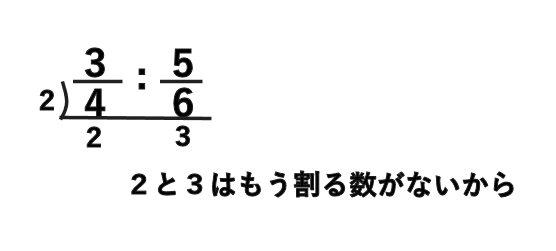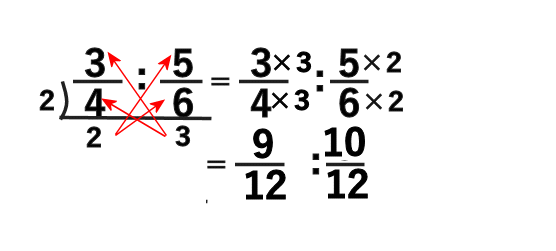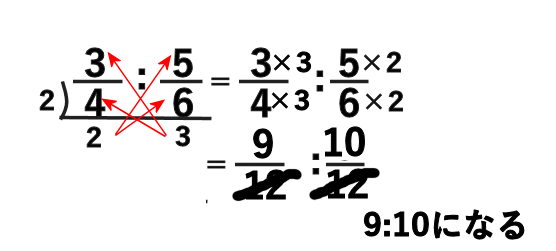



分数の比を簡単にする




練習問題アリ 分数の通分を習得しよう やり方や最小公倍数を簡単に計算するコツも解説 学び通信
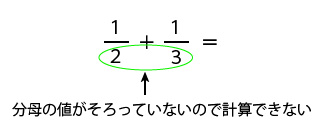



通分と約分 もう一度やり直しの算数 数学



5年算数分数のたし算ひき算の教え方 異分母
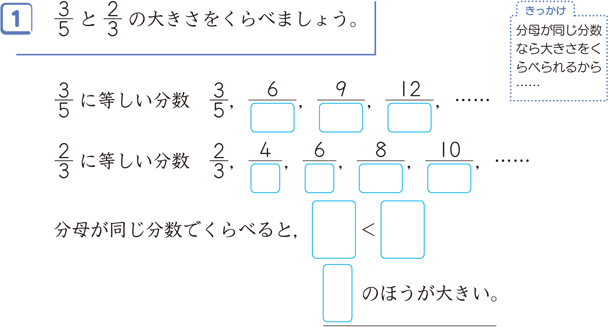



通分と約分 算数用語集




算数 分数を通分するときの最小公倍数を簡単に見つける方法を解説 数スタ



通分のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料
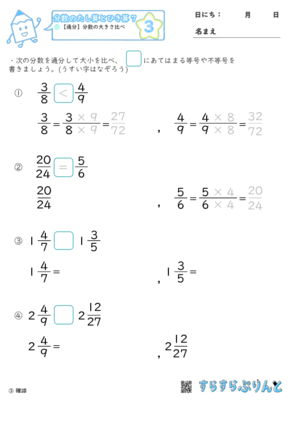



通分 分数の大きさ比べ 小学4年生算数 無料プリント教材



5年算数 通分約分の仕方
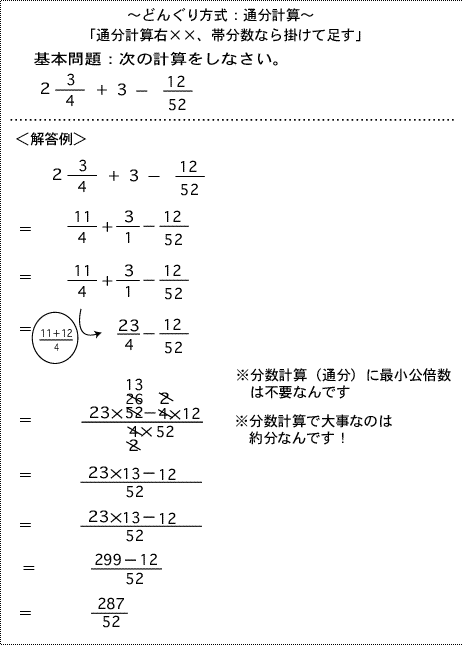



分数が分からない理由




分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト
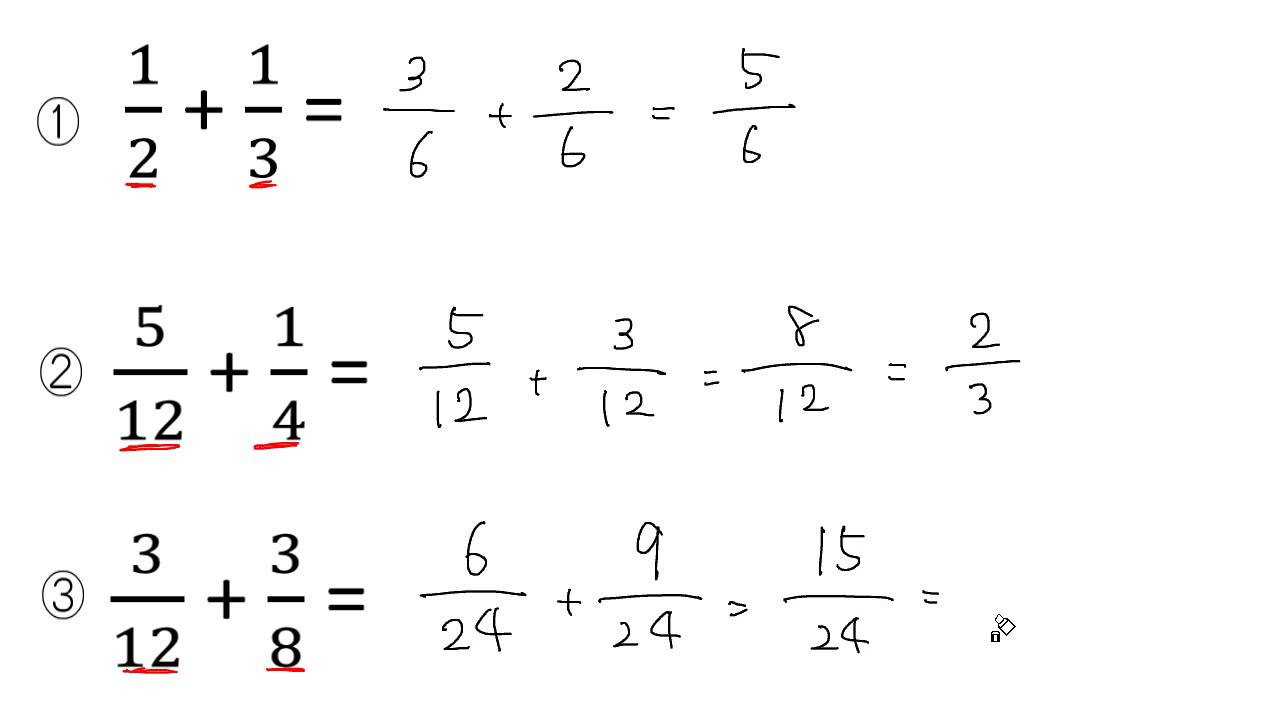



分数の足し算 引き算 通分あり Youtube



算数 分数の約分のしかた 教え方のコツ なるほど 塾講師が教える教え方のコツ
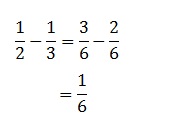



算数 分数の通分 やり方のコツ なるほど 塾講師が教える教え方のコツ




分数の大小関係 通分や小数にするのが解き方のコツだ 中学や高校の数学の計算問題



5年算数 通分約分の仕方
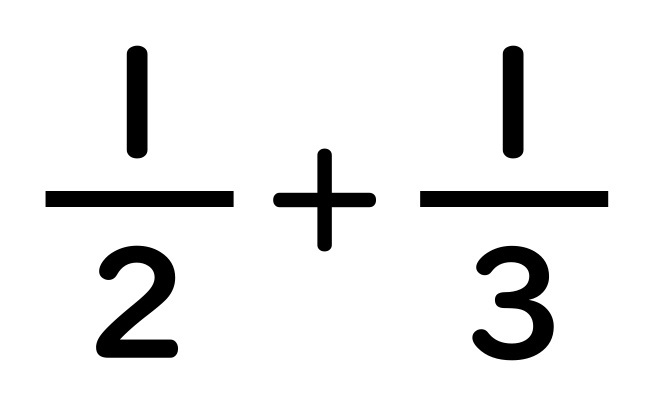



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説
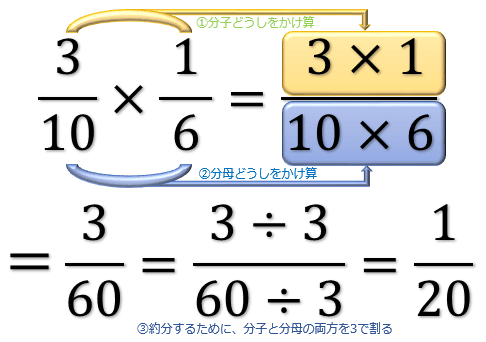



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




通分 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




小5 算数 小5 35 分数 通分 Youtube
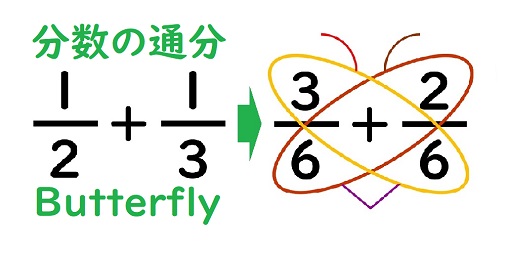



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説



5年算数 通分約分の仕方



通して使える通分のやり方 教育考現学



1



通分のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




中1数学 正負の数 分数計算のやり方を問題解説 数スタ




通分 3つの分数の通分 小学5年生算数 無料プリント教材



1




小学生向け 算数 プリント 分数の通分 小さい数 学習塾 Step By Step



通分とは何か 通分をマスターして分数計算をスピードアップする方法 中学受験ナビ
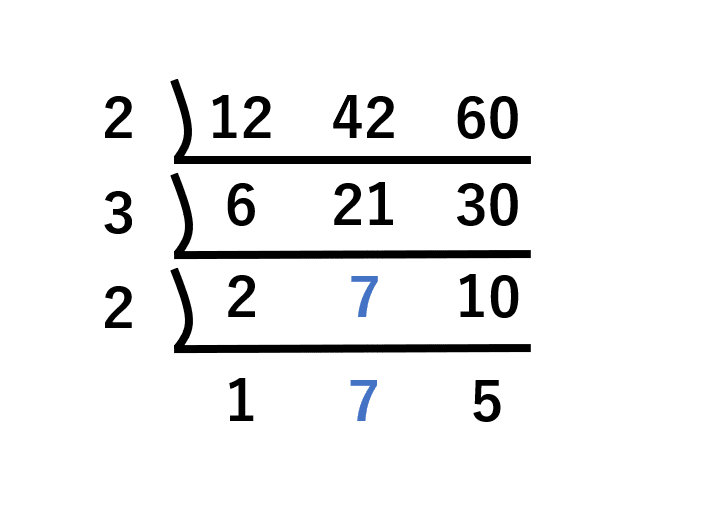



練習問題アリ 分数の通分を習得しよう やり方や最小公倍数を簡単に計算するコツも解説 学び通信
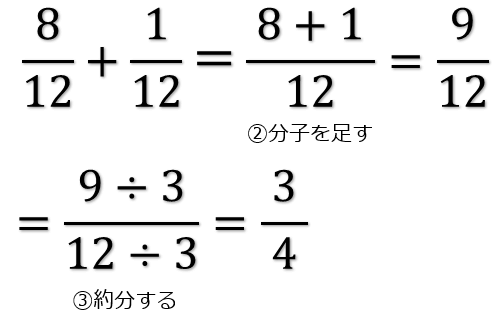



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




Books Kinokuniya 小学5年生約分 通分をする分数の計算 改訂1版 くもんのにがてたいじドリル算数



1




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun




小学生向け 算数 プリント 分数の通分 大きい数 学習塾 Step By Step




通分と約分 算数用語集



3つの分数の通分は 1分でわかる計算方法 3つの分数の掛け算 例題
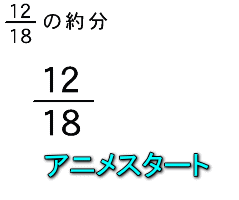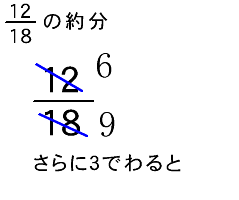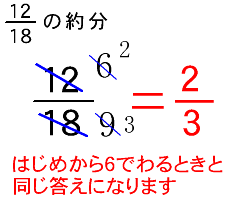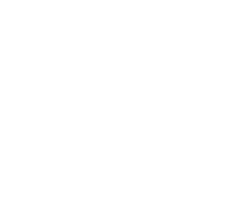



5年算数 通分約分の仕方
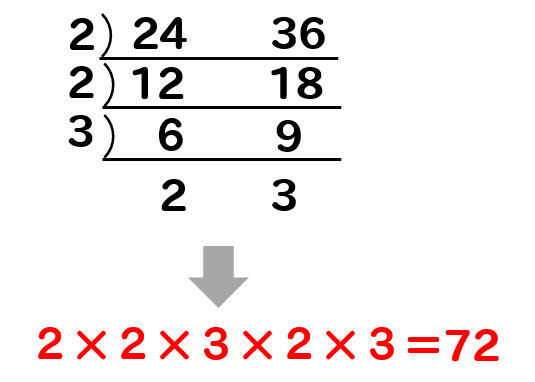



算数 分数を通分するときの最小公倍数を簡単に見つける方法を解説 数スタ




算数 分数を通分するときの最小公倍数を簡単に見つける方法を解説 数スタ




分数ってなぜ比べにくいの 通分の仕方がわかれば分数の計算も簡単に 中学受験ナビ




通分 問題練習 Youtube




分数の足し算 引き算は通分してもしなくても同じ値 Okwave



通分の仕方 導入 教育考現学




小学5年生 分数の約分




分数の約分 約分の仕方を元塾講師が解説 通分との違いも トムラボ
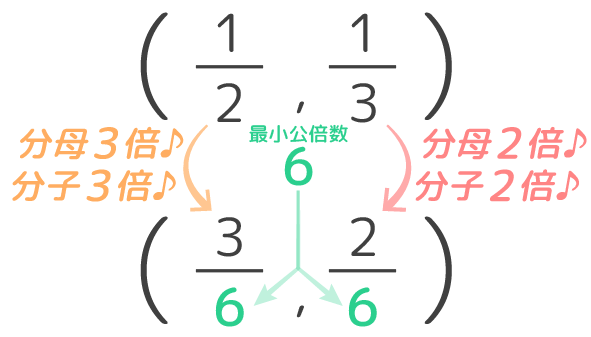



何年生で 分数の通分のやり方教え方と問題演習 3つの分数の通分も そうちゃ式 分かりやすい図解算数 別館




通分のやり方 算数 Youtube



異分母の引き算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




通分のテクニック デキる人はやっている 通分をラクにする方法 子供から大人まで動画で脳トレ 楽天ブログ




分数の計算のやり方 一覧 小学生 中学生の勉強



佐屋小学校



通分のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料



通分 問題練習 Youtube
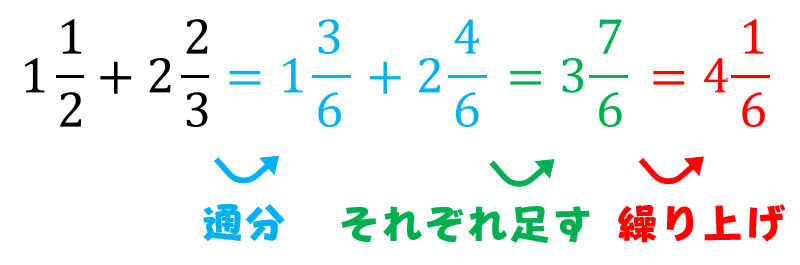



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun



5年算数 通分約分の仕方




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun




分数の計算方法を解説 分数は小数よりもずっとサボれる



3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく




分数の多項式の足し算や引き算 通分してからがポイントだ 中学や高校の数学の計算問題




世界一分かりやすい算数 小5 分数 1



通分と約分 もう一度やり直しの算数 数学



約分 通分のポイント シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




分数のひき算 やり方を解説 足し算と通分 約分も 工学博士監修 トムラボ



2
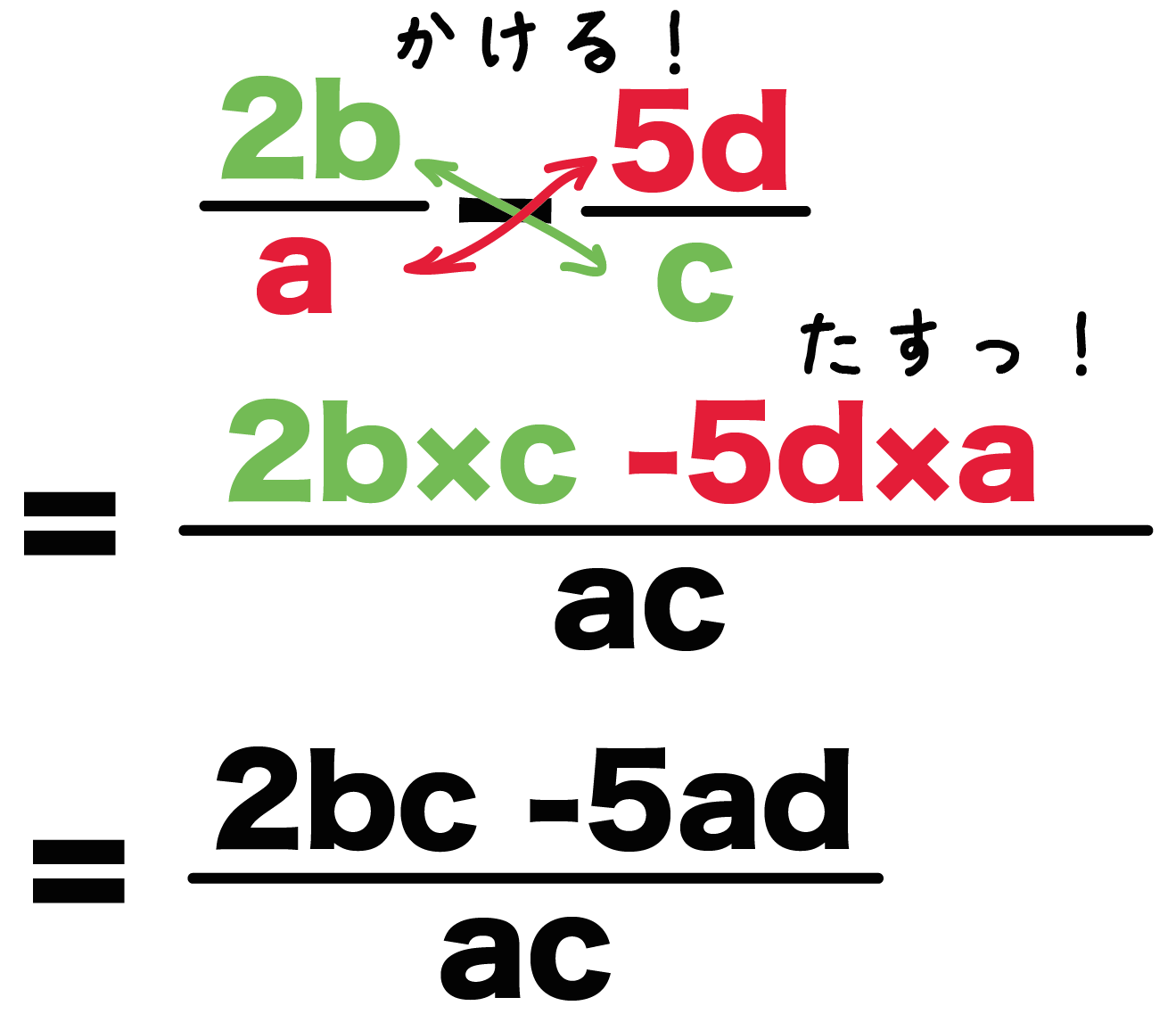



3分でわかる 分数の文字式の通分方法 Qikeru 学びを楽しくわかりやすく




小学生向け 算数 プリント 分数の通分 大きい数 学習塾 Step By Step



分数の割り算に通分を使う トトロのパソコン珍道中



3つの分数の通分は 1分でわかる計算方法 3つの分数の掛け算 例題




4 3 式の計算 通分のやつ 勉強できようサイト



1



すきるまドリル 小学5年生 算数 分数のたし算とひき算 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント




帯分数の足し算 通分あり Youtube
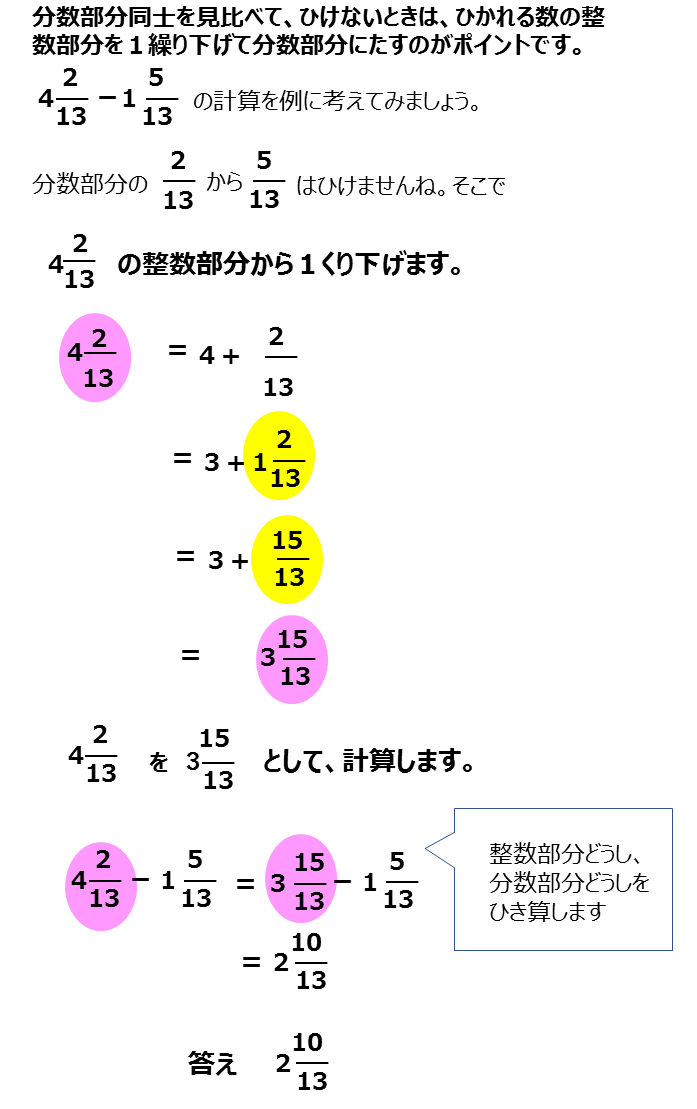



帯分数のひき算 小学生の算数質問ひろば 進研ゼミ小学講座




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




小学5年生の算数 動画 分数の技 通分編の問題 19ch




分数の足し算や引き算の問題 通分できるかが非常に大切 中学や高校の数学の計算問題




4 3 式の計算 通分のやつ 勉強できようサイト




すきるまドリル 小学5年生 算数 分数のたし算とひき算 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント
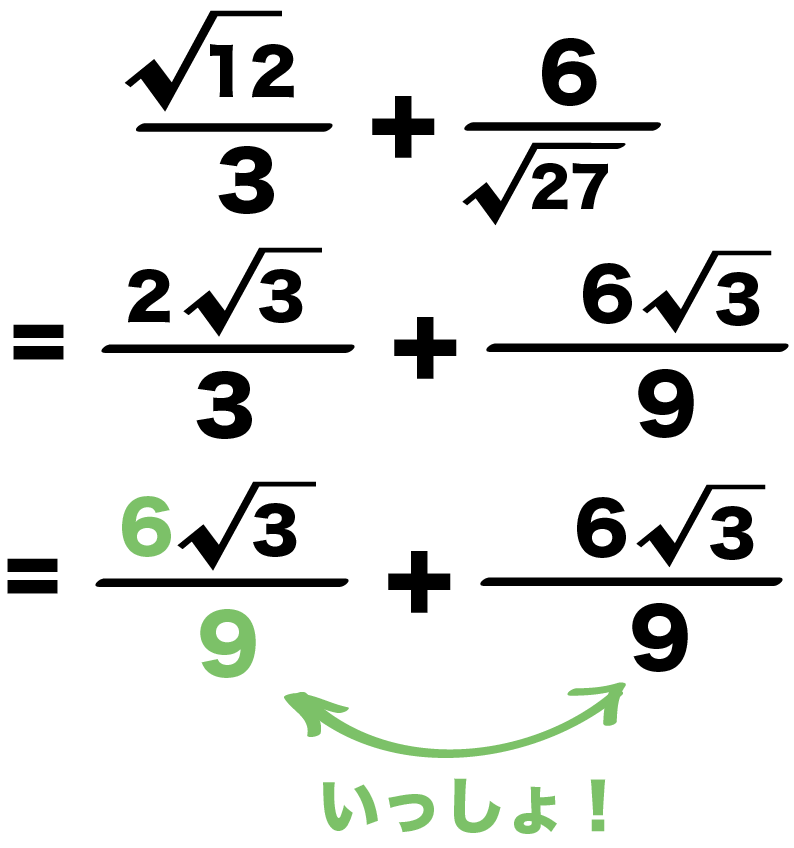



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



簡単 分数の通分 苦手な人向け計算テクニックを丁寧解説



通分のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun



通分とは 1分でわかる意味 足し算と引き算の問題 最小公倍数との関係




小学校5年生の算数 数学fun 小学校 算数 勉強 本 数学



0 件のコメント:
コメントを投稿